le projet a été développé dans l'unité 483 inserm, sous la direction d'yves burnod. le programme crée fait partie des outils développées pour mon actuel (juin, 1999) projet de thèse.

le modèle anatomo-fonctionnel du cortex humain déplié est un modèle géométrique simple de l'anatomie et des quatre principales aires fonctionnelles du neocortex humain. le modèle est né de l'étude de la surface cortical par des techniques de dépliement virtuel (reconstruction, lissement, deformations élastiques) a partir d'imágenes par resonance magnetique nucléaire.

Après 20 ans d'utilisation de techniques manuelles pour le dépliement du cortex, plusieurs équipes ont développé des systèmes de reconstruction et dépliement par ordinateur de larges extensions de cortex (Dale et Sereno, 1993; Carman et al., 1995; Sereno et al., 1995; DeYoe et al., 1996; Drury et al., 1996), et aussi le premier atlas du cortex déplié (Van Essen et al., 1997)1.

Le projet de stage développé ici, le modèle du cortex humain déplié, se fait dans le contexte d'une étude de la plasticité des voies visuelles chez les sujets atteints de dégénérescence maculaire liée à l'age. Ce projet se trouve non seulement lié à l'étude physiologique de la rétinotopie sinon aussi aux travaux de modélisation du laboratoire INSERM CREARE. Ainsi, on a cherché développer un modèle simple du cortex déplié pour mieux comprendre les données fonctionelles dans son contexte anatomique. La construction de ce modèle implique le développement des techniques de reconstruction de la surface corticale, de dépliement et de mapping des images d'IRMf sur le modèle.

Dans la première partie du mémoire, on va aborder le problème qui donne lieu au projet de stage, celui des caractéristiques dynamiques de l'organisation des cartes corticales des aires visuel, et les particularités de cet étude chez l'humain. Ce sont ces particularités qui rendent nécessaire la création d'un modèle déplié du cortex. Dans la deuxième partie du mémoire on va présenter le problème général du dépliement du cortex, en commençant par une synthèse sur le développement du cerveau. On abordera aussi dans cette partie les techniques de dépliement virtuel du cortex. Enfin, on montrera les techniques de dépliement virtuel qui ont été développées et le modèle anatomo-fonctionel du cortex humain déplié qui elles aident à générer.

En particulier dans le cortex visuel des primates non-humains, qui occupe plus de la moitié de son neocortex, on peut identifier au moins 25 différentes aires, plusieurs d'entre elles ayant un certain degré d'organisation rétinotopique. Chez l'humain les aires visuelles occupent aussi une large portion du neocortex, cependant, l'étude des aires visuelles humaines a été difficile avec seulement des techniques non invasives. Ainsi, pour ce qui est de l'étude des caractéristiques de l'organisation rétinotopique des aires visuelles, les travaux ont été principalement développés chez des animaux.

Dans cette première partie du mémoire, on va présenter quelques aspect théoriques sur l'organisation des cartes corticales. Ces études ont été principalement développés chez l'animal. En suite, on montrera le contexte qui donne lieu au projet de stage, l'étude de la plasticité et adaptation des voies visuelles chez les sujets atteints de dégénérescence maculaire liée à l'age. Ce dernier projet se montre comme une alternative intéressante pour ce qui est de l'étude de l'organisation corticale chez l'humain.

Dans son article de synthèse Horizontal Integration and Cortical Dynamics de 1992, C.D. Gilbert présente une vision dynamique des concepts de champ récepteur et de carte cortical. Cette nouvelle conception, souligne Gilbert, a affaire directement avec notre compréhension des processus perceptifs.

Traditionnellement, l'image des premières étapes de traitement sensoriel a été celle d'une architecture fixe, la capacité d'adaptation aux changements de l'environnement sensoriel étant donc une caractéristique des aires corticales supérieures. Gilbert propose que cette image est en train de changer vers une conception beaucoup plus dynamique des champs récepteurs et de la topographie corticale, un phénomène qui peut être déjà observé dans les aires sensoriels primaires.

Le concept de champ récepteur est un concept central en physiologie corticale. Le champ récepteur d'une cellule est la partie du champ visuel dans laquelle un stimulus particulier, comme un petit trait, peut causer l'activation de cette cellule. Dans tout le cortex visuel il y a un mapping systématique du champ visuel sur la surface de chaque aire corticale visuelle. Chaque cellule du cortex visuel, depuis la pia mater jusqu'à la matière blanche, souligne Gilbert, a son champ récepteur.

Le point de vue traditionnel suggère que chaque image sur le cortex visuel est analysée pour essayer de reconnaître des objets à partir de caractéristiques élémentaires comme l'orientation de ses bords ou sa curvure. Ce processus d'atomisation d'un objet en des petits trait mène au problème du liage de ces traits dans une perception unifiée, la perception d'un visage par exemple. A coté de cette vision de champ récepteur comme un type de filtre statique, Gilbert montre une autre conception de champs récepteurs qui a affaire avec la question sur la perception.

Gilbert affirme que les caractéristiques des champs récepteurs ne sont pas fixes, sinon qu'elles dépendent des stimuli, et que même les stimuli situées hors du champs récepteur d'une cellule peuvent moduler sa réponse. Donc, la réponse pour une image complexe ne peut pas être prédite par la réponse aux stimuli plus simples. Si une vision antérieur suggérerait que cette intégration a lieu dans les aires visuelles supérieures, maintenant les évidences font penser que même dans le cortex visuel primaire les cellules sont capables de faire des intégration sur des larges portions du champ visuel.

Ce caractère dynamique de l'organisation corticale a été aussi souligne par Merzenich (Merzenich et al., 1984) sur la base de ses expériences dans le cortex somatosensoriel du singe. Le cortex somatosensoriel a un mapping qui dépend de la position dans la surface du corps, de la même façon que les cartes visuelles ont un mapping qui dépend de la position dans le champ visuel. A travers de l'amputation d'un ou deux doigts de la main d'un singe, Merzenich élimine une entrée sensoriel, ce qui laisse une région du cortex somatosensoriel dans le silence. Après un certain temps, le fonctionnement de l'aire silenciée change, et elle développe une représentation d'une partie différente du corps. Ces changements font conclure à Merzenich que les frontières entre différentes régions d'une carte corticale sont maintenues d'une façon dynamique.

Ces expériences sur la dynamique de l'organisation corticale peuvent trouver son parallèle dans celles faites chez l'être humain atteint d'une dégénérescence maculaire liée à l'âge (dmla). La dmla représente la cause la plus importante de basse vision acquise dans les pays occidentaux. L'augmentation de son occurrence est directement liée à l'âge moyen de vie d'un individu. Cette pathologie qui se caractérise par une perte progressive de la vision centrale par dégénérescence sénile de la macula a comme résultat final la desafférentation d'une région importante du cortex visuel.

Les équipes de J-F Le Gargasson et de A. Gaudric ont effectué de nombreux travaux sur la dmla. Ils ont montré, à l'aide d'un ophtalmologue laser à balayage, que 70% des sujets dont la surface rétinienne maculaire n'est plus fonctionnelle, choisissent une nouvelle aire de fixation située en bordure de la lésion: celle-ci réalise l'analyse fine de la scène visuelle normalement dévolue à la macula.

L'objectif du projet est de suivre, chez l'homme atteint de dmla, le processus de réorganisation des aires corticales visuelles. Dès que le cortex visuel primaire se trouve presque complètement enfoui dans les profondeurs du sulcus calcarin, et à cause de l'extreme variabilité du parcours et configuration de ce sulcus (voir Damasio, 1995), le dépliement du cortex a une importance fondamental pour la comparation et la compréhension des données.

La modélisation des voies thalamo-corticales peut être utilisée pour prédire la récupération des capacités visuels élémentaires suit à une scotomisation de la rétine, sur les bases de la plasticité synaptique local. L'équipe de travail en imagerie et modélisation de l'INSERM Unité 483 a simulé des architectures neurales qui pourraient rendre compte de ces phénomènes (Koechlin, Anton et Burnod, sous presse), et ses prédictions ont été testées avec succès dans plusieurs situations adaptives. Pour lier les aspects expérimentaux de l'évolution de l'organisation des aires visuels et les travaux de modélisation, il est nécessaire la construction d'un modèle anatomo-fonctionel simple du cortex humain.

Dans cette deuxième partie du mémoire, on va aborder le développement du cortex, et puis on montrera les différentes techniques par lesquelles le dépliement de la surface corticale a été essayé.

L'embryon des mammifères est formé principalement par trois couches de cellules: l'endoderme, le mésoderme et l'ectoderme. Cette dernière couche, l'ectoderme, va donner lieu à tous les tissus du système nerveux central et périphérique, elle originera aussi l'épidermis.

Une région spécialisée de l'ectoderme, la plaque neural, origine les neurones et les cellules gliales. La plaque neural, dans les procès de la neurulation, va se plier pour former une structure connue comme le tube neural. La cavité à l'intérieur du tube neural origine le système ventriculaire, et les cellules épiteliales dans les parois du tube génèrent les neurones et cellules gliales du système nerveux central.

Pendent ces premières étapes du développement neural, les cellules se divisent très rapidement. Cette prolifération n'est pas uniforme le long du tube neural, et cette expansion différentiée donne lieu aux plusieurs régions spécialisées du système nerveux central adulte. Ainsi, la partie caudal du tube neural origine la moelle épinière et la partie rostral origine le cerveau.

Dans les premières étapes du développement il est possible différencier dans la partie rostral du tube neural trois vésicules: le prosencéphale, le mésencéphale et le rombencéphale. En plus, dans ces étapes le tube neural se fléchisse dans deux points: le fléchissement céphalique, dans l'union entre mésencéphale et rombencéphale; et le fléchissement cervical, dans l'union entre le rombencéphale et la moelle épinière. Un troisième fléchissement apparaît plus tard dans le développement, le fléchissement pontine. Seul le fléchissement céphalique demeure dans le développement jusqu'à la maturité.

Plus tard dans le développement, le prosencéphale se subdivise en télencéphale et diencéphale. Le télencéphale origine les hémisphères cérébraux, l'hypocampe et l'amygdale; le diencéphale origine le thalamus, le subthalamus, l'hypothalamus et la rétine. Le rombencéphale se subdivise en métencéphale et myélencéphale. Le métencéphale origine le pédoncules cérébraux et le cervelet. Le myélencephale origine la moelle.

Finalement, les hémisphères cérébraux vont se développer jusqu'à ce qu'il vont couvrir la plupart du diencéphale et du mésencéphale. Les circonvolutions du cortex seront un effet de l'incrément supérieur de son volume en comparaison avec le volume crânien. Cependant, la croissance des hémisphères n'étant pas homogène, il y a certaines plissements avec une courbure intrinsèque, et non pas uniquement des plissements dus aux différences de volume.

Ces courbures intrinsèques ont été pendent longtemps la principal difficulté qui ont dû résoudre les techniques de dépliement de la surface cortical.

Les premiers travaux faites sur des régions plates du tissu cortical datent de 1970, quand Woolsey et Van der Loos ont fait des analyses histologiques de sections parallèles à la surface du cortex somatosensoriel du rongeur. Puis, cette méthode fut utilisée pour examiner les patterns de connexion de plusieurs aires du cortex (Shatz et al., 1977; LeVay et al., 1980). En 1974, Welker et Woolsey améliorent la technique en aplatissant les hémisphères cérébraux avant de sectionner, ce qui permettait d'analyser des larges aires de cortex somatosensoriel de rongeur dans une seule section tangentielle.

Cependant, la méthode était difficile à appliquer aux tissus trop repliés, ce que limitait son usage aux cerveaux lisencéphaliques, ou à des régions petites et naturellement plates des cerveaux gyrencéphaliques (ex. Wise et Jones, 1976; Olavarria et Montero, 1984). Une des plus grandes difficultés est que dans les cerveaux gyrencéphaliques la matière grise du cortex n'est pas simplement une surface plate pliée, dans plusieurs régions il y a une courbure intrinsèque, comme dans la surface d'une sphère.

Une deuxième méthode a été développée par Gattas et Gross (1981). Un modèle tridimensionnel d'une région du cortex est construit en fil de fer, ou chaque section est représentée par un fil. L'espacement adéquat est conservé par moyen de morceaux de fil croisé soudés. Après, le modèle est physiquement aplati, ce qui demande à couper des fils de contour et aussi des fils croisés. Dès que la surface définie par un modèle un fil de fer n'est pas élastique, des nombreuses coupures sont exigées.

La troisième méthode a été utilisée pour des primates (Tootell et Silverman, 1985) et des chats (Olavarria et al., 1985; Freeman et al., 1987). D'abord le cerveau est faiblement fixé, ou ne pas fixé , et l'arachnoïde est incisée. Puis, la matière blanche est séparée de la matière grise et on introduit quelques coupures le long des marges du cortex. La surface de tissu résultant est soigneusement pressée entre deux plaques de verre pour la maintenir plate. Après, le tissu est gelé et coupé tangentiellement. Les patterns gyraux des cerveau intactes donnent des importants points de repère pour déterminer la position de plusieurs aires corticales. Pour préserver ces points de repère dans le tissu aplati, avant de déplier, le cortex est trompé dans une solution qui laise dans le cortex aplati une représentation des patterns gyraux.

Récemment, une quatrième type de méthode a été proposé qui utilise des ordinateurs pour un dépliement virtuel de la surface cortical. Contrairement aux techniques sur des tissus réels, comme celles de Olavarria et Woolsey, les techniques de dépliement par ordinateur ne permettent pas l'étude de la connectivité des tissus neuraux. Cependant, avec l'arrivée des études d'imagerie cérébral, cette dernière type de méthode acquière une toute nouvelle importance, et elle se montre comme l'unique alternative pour le dépliement du cortex humain.

Pendent les dernières années, différentes techniques ont été proposées pour la génération automatique de cartes dépliées du cortex par ordinateur. Carman (Carman, 1995) fait une distinction de ces techniques selon la façon dont il traitent les relations géométriques de la surface cortical. La méthode la plus simple est celle du relâchement (Acton, 1970; Young, 1971), qui implique le lissement itératif de la surface cortical. Cette méthode garde uniquement les relations de voisinage (Dale et Sereno, 1993; Carman et al., 1994).

Les trois méthodes de dépliement virtuel les plus utilisées actuellement sont les développées par Wandell à l'Université de Stanford (Wandell et al., 1996), Carman et Drury (Carman et al., 1995; Drury et al., 1996) à l'Université de Washington et Dale et Sereno à l'Université de Californie (Dale et Sereno, 1993). Habituellement ces méthodes de dépliement par ordinateur impliquent trois étapes: la numérisation des contours, la reconstruction de la surface et, enfin, le dépliement. Cependant, la forme de chacune de ces étapes varie beaucoup d'une implémentation à l'autre, ce qui fait les avantages et désavantage de chacune des méthodes.

Le système développé par Brian Wandel, mrGray pour la reconstruction et mrUnfold pour le dépliement est partiellement disponible par internet. Ces logiciels ont été utilisées pour étudier l'organisation rétinotopique dans le cortex visuel humain (Engel et al., 1996) et font partie (seulement mrGray) de l'étape de reconstruction de surface du système CARET3 (Computarized Anatomical Reconstruction and Editing Toolkit, Drury et Van Essen, 1997).

Le problème de la numérisation de contours et de la reconstruction de la surface a été astucieusement abordé par Wandel. D'abord, une détection semi-automatique de la matière grise se fait au niveau tridimensionnel ( par des pas de 3 coupes adjacentes à la fois). Après, le logiciel choisit d'une façon aléatoire un ensemble de points appartenant à la matière grise. Les points ont une séparation minimale (résolution du sampling) choisie par l'utilisateur. Les positions des points dans le modèle original sont enregistrées pour guider l'algorithme d'aplatissement.

L'algorithme d'aplatissement essaye de déplacer chaque point vers un plan ( d'habitude un plan de vecteur normal (0,0,1) ) en respectant les distances enregistrées aux points du voisinage. Chaque voisinage est formé par une certaine quantité de points (d'habitude 20) qui rentrent dans une sphère de radius choisit par l'utilisateur. De cette façon, il n'y a plus besoin d'indiquer la forme dont les points vont s'unir les uns aux autres (il n'y a pas de noeuds, uniquement des points), un processus compliqué et qui demande beaucoup d'intervention de l'utilisateur.

Cependant, actuellement mrUnfold est un logiciel pour l'aplatissement de régions du cortex et non pas pour le dépliement général du cortex. La méthode pour éviter la génération d'un réseau de noeuds demande le stockage d'un ensemble très important de points pour assurer la conservation des relations de distance et de forme ( les angles entre noeuds).

L'algorithme de dépliement utilise trois différents forces pour accomplir sont but: une force élastique (force interne) pour garde la taille des bords, une force de dépliement qui essaye déplacer chaque point vers le plan définit par ses voisins et une force de torsion pour conserver les angles entre noeuds. Carman appelle ces dernières des forces externes. Le déplacement total de chaque point est calculé comme une fraction de la somme des forces internes et externes, ce qui évite des instabilités dans le processus de dépliement.

Dans certaines zones où la surface cortical est trop convolutée, les forces font la surface se plier sur elle même. Pour résoudre ce problème l'algorithme utilise une premier étape de lissement. Cette étape diminue la taille global de la surface ce qui est compensé par un agrandissement homogène. En plus, on inclut une étape où les forces de dépliement sont appliquées uniquement aux point externes de la surface tridimensionnelle, et on lisse ses point internes.

Cet algorithme permet un dépliement général du cortex en gardent les distances originales et les angles (donc, l'aire). Cependant, l'utilisation d'une force de dépliement qui dépende uniquement des points voisins peut introduire des instabilités dans le processus.

Dans cette troisième partie du mémoire on va présenter les techniques développées pour la reconstruction tridimensionnel du cortex, pour son dépliement et pour le mapping. Enfin, on va exposer les résultats obtenus par ces techniques, et le modèle anatomo-fonctionel du cortex humain déplié qu'elles aident à générer.

Le processus de génération d'un modèle tridimensionnel de la surface cortical à partir d'un ensemble de coupes deuxdimensionnelles comprends principalement ces deux pas:

i. tracer pour chaque coupe des courbes de segmentation qui séparent les pixels qui appartiennent à la matière grise de ceux qui font partie de la matière blanche, et

ii. connecter et unir les courbes dans des coupes adjacentes, ou dans la même coupe (cas de l'union entre une courbe et un trou).

Comme résultat de ces deux pas on obtient un ensemble connecté de noeuds dans l'espace tridimensionnel qui modèle la surface du cortex.

Plusieurs méthodes existent pour la segmentation automatique de la matière grise, cependant il y a toujours nécessité d'une certaine quantité de ajustement manuel. On a choisi créer d'abord une version complètement manuel de segmentation de la matière grise, c'est à dire, des méthodes de manipulation et visualisation des segmentations, et laisser pour un développement postérieur l'inclusion de méthodes de segmentation automatique.

Le tracé de la matière grise se fait avec la souris ( ou éventuellement avec une tablette graphique ) sur l'image des sectionnes horizontales du cerveau. Pour guider le tracé, le logiciel développé peut générer dans chaque point de l'image de irm une reconstruction de la section sagittal ou coronal associée. Un algorithme a été développé qui approxime ce tracé par une courbe de Bézier. Le recours à ce type d'approximation permet un stockage des segmentations avec indépendance de la résolution des coupes de irm ou de la résolution de la discretisation des courbes.

Il y a deux types particuliers de contour qui doivent être étiquetés. Le premier cas se produit quand l'image de irm coupe tangentiellement la surface du cortex. Dans ce cas-là, la courbe segmentée ne doive pas être connectée avec l'image suivante, pour cette courbe tangentielle il faut générer une triangulation interne. Le deuxième cas se produit pour les courbes qui représentent un trou. Ces courbes doivent être connectées avec une autre courbe dans la même coupe.

Par connexion de deux courbes on entend le processus d'association de ces courbes entre deux coupes adjacentes par moyen d'un trait guide. La connexion des courbes peut se faire sur les courbes non-discretisées, et elle est donc, indépendante de la résolution.

Par union de courbes on entend le processus d'assigner à chaque point d'une courbe discrétisée un ou plusieurs points d'une courbe adjacente. L'union de ces deux courbes est dépendante de la résolution choisisse. La résolution de la discrétisation d'une courbe détermine la quantité total de points du modèle, et elle est donc contraintée par les capacités de mémoire de l'ordinateur.

Quatre différents types de connexion et union de courbes peuvent se produire: a. entre deux courbes simples, b. entre une courbe et un trou, c. entre une courbe et plusieurs courbes, et enfin, pour une seule courbe, d. sa triangularisation interne.

Dans le cas le plus simple, la connexion et l'union de deux courbes se limite à la discrétisation des courbes et à l'union automatique de ses points par un algorithme qui rejoint les points selon un critère de prochaineté. L'algorithme prends comme points de départ les deux points extrêmes du trait guide qui connecte les deux courbes à unir, puis il compare les distances de ces point aux points suivantes dans chaque courbe. Si la distance à un des points est mineur que l'autre, ces deux point vont être unis. L'algorithme continue avec ce nouveau point comme un des points de départ. Contrairement, si les deux distances sont égales, l'algorithme prends alternativement un des deux points pour conserver la triangularité de l'union. Cette triangularité de l'union va permettre après, dans l'étape du dépliement, la conservation de l'aire de chaque triangle du modèle tridimensionnel du cortex dans le modèle déplié. Si tous les polygones utilisés sont des triangles et la taille de ses bords ne varie pas, la forme (le rapport entre les angles des sommet des polygones) se conserve sans nécessité d'une force de torsion, comme celle de l'algorithme de Carman.

Dans toutes les courbes, les point sont automatiquement ajoutés de façon à conserver un même sens de tournure. Ce sens de tournure définit en chaque point la direction du vecteur normal à la surface modélisée. Parfois, un repliement de la surface du cortex peut générer un trou, comme le montre la figure x. Les trous sont connectés et unis de la façon habituel, sauf que ses points doivent être ajoutés dans un sens de tournure qui dépende de la courbe "solide" à laquelle le trou appartient.

Un autre problème de la génération d'un volume à partir de coupes deuxdimensionelles est celle des branches (figure x). Une nouvelle extension des traits guides à été utilisée pour résoudre ce problème. Cette fois, les traits rectilinéaires ont été généralises à une ligne, sans restrictions d'allure, qui sert à diviser une courbe en des branches. Les lignes sont approximées par des courbes de Bézier ouvertes, puis elles sont discretisées et ses points unis aux courbes adjacentes de façon à respecter le sens de tournure.

Pour les sections tangentielles, il faut générer une segmentation interne, dont le sens d'union des points du bord de la section dépend, comme dans le cas précédant, de cette courbe. La méthode développée génère une segmentation homogène de l'intérieur de la courbe qui dépends uniquement de la résolution choisisse. Les points du bord de la courbe sont unis aux points internes les plus proches.

Dans chaque étape de la reconstruction, pour vérifier la rectitude du modèle, il est possible générer une union partiel du niveau actuel. Enfin, on génère une union général du modèle, ce qui donne la reconstruction tridimensionnel. On a crée des outils pour la visualisation de cette surface, et pour son exportation à des systèmes de modélation tridimensionnel standard.

Les deux algorithmes agissent sur une surface triangularisée à laquelle on a ajouté un coefficient dit d'élasticité. Etant l'aire d'un triangle déterminée par la taille de ses bords, on conserve l'aire de la surface original et sa forme par moyen de cette coefficient d'élasticité. Le premier pas pour le dépliement c'est donc le stockage des longueurs initiaux.

Pour chaque point de la surface l'algorithme calcule, en fonction des points voisins, l'équation du plan d'aplatissement. Le plan d'aplatissement c'est le plan qui rendrait plate cette parti de la surface. Ce plan est calculé par le moyenage de tous les plans possibles de faire avec une combinaison de trois points voisins, chacun des plans pondéré par son aire.

La magnitude et direction du déplacement de chaque point de la surface dépends de la distance du point au plan d'aplatissement plus le déplacement causé par l'élasticité de la surface.

Quoique l'algorithme fonctionne bien pour des surfaces simples, les forces locales d'aplatissement peuvent induire des déplacements qui s'opposent entre différentes partis d'un même surface. Cependant, cet algorithme, similaire à celui utilisée par Wandel et par Carman, est capable de rendre une surface plate.

Pour évité les "contradictions locales" du premier algorithme, on a cherché une façon de déplier un surface avec une force global, qui rendrait le dépliement indépendant des particularités locales de la surface. Ce deuxième algorithme est similaire au précédant, sauf que la direction du déplacement c'est tout le temps vers le coté externe de la surface, et sa magnitude est fixé par un coefficient dit de gonflage. Ce type de processus peut être en fait assimilé au "gonflage" de la surface.

En agissent sur les coefficients d'élasticité et de gonflage on peut contrôler le depliement de la surface et puis la constance de l'aire (le gonflage et le dégonflage).

Il est nécessaire pour le fonctionnement de l'algorithme que la surface soit un volume, à différence du premier algorithme qui peut travailler sur une surface. Un problème de cet algorithme est la production de "vésicules" pour certaines convolutions trop prononcées. Ce problème se résoud avec un faible gonflage et élasticité dans les premières étapes, et aussi avec l'alternance de séquences de gonflage et dégonflage.

Ainsi, on a coloré sur les coupes de irm, à l'aide des atlas de Talairach (Talairach, 1988) et de Damasio (Damasio, 1995), les aires frontal, pariétal, temporel, et occipital du cortex humain, puis on a fait le mapping de ces zones sur le modèle de surface corticale dépliée.

Un modèle de l'hémisphère droit d'un cerveau a été reconstruit à partir des données obtenus d'une machine de irm Siemens de 1.5 [Tesla]. Le cerveau a été numérisé dans un ensemble de 124 coupes sans espacement, la taille de chaque voxel étant 1.3x1.3x1.1[mm]. Le protocole a été choisit pour maximiser le contraste entre matière blanche et matière grise, cependant la très mauvaise qualité des images (le niveau de gris le plus haut n'étant jamais supérieur à 100 pour une machine de irm de 16bits de résolution) a fait très difficile le tracé des courbes de segmentation. A cause de ce problème, cette segmentation aurait été impossible avec un algorithme automatique.

Pour la reconstruction on à tracé 238 courbes, 836 traits guides et 49 lignes. La discretisation a été faite avec une résolution de 50/16 pixels, c'est à dire 3.125 [mm], ce qui donne un total de 24422 points et 48329 triangles après la reconstruction. A cause de la très mauvais qualité des images, le travail de tracé à été très difficile et lente ( 5 jours entiers, et les ajustements postérieurs ). De la même façon que Van Essen (Van Essen et al. 1997), on a fermé artificiellement les points naturels de terminaison du neocortex (l'union avec le corpus callosum).

L'imprécision des tracés à la main introduit des imperfections dans les modèle tridimensionnel. Sur la base de l'algorithme de dépliement local, qui essaye de rendre une surface localement plate, on a développé une méthode de lissage qui élimine les composants de "plus haute fréquence" du modèle tridimensionnel.

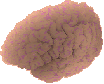
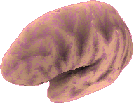
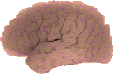
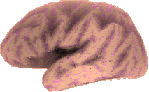
Le dépliement du modèle a été fait en plusieurs étapes qui peuvent, cependant, être rassemblées en trois: une première étape de gonflage et d'élasticité très faible pour éviter les problèmes caractérises antérieurement; une étape de forte gonflage et grand élasticité, pour déplier rapidement la surface; et enfin une étape de faible vers nulle gonflage et très faible élasticité, pour récupérer l'aire original du modèle. Les images montrent deux vues du cortex reconstruit plié et déplié. Il a été fait le mapping de la profondeur rélative de sillons et de la courbure de chaque point.

C'est intéressant de remarquer que dans les premiers étapes du développement du système nerveux la surface d'un hémisphère cérébral a une allure plutôt sphérique. Dans ce modèle déplié d'un hémisphère cérébral adulte, on peut observer l'importante croissance sur tout du lobe temporel, mais aussi celle des lobes frontal et occipital qui éloignent cette surface de la sphère original.

A l'aide des atlas de Talairach (Talairach, 1988) et Damasio (Damasio, 1995) on a coloré sur la surface dépliée du cortex de cet hémisphère ses quatre principales aires anatomo-fonctionels. En rouge le lobe frontal, en vert le lobe pariétal, en jaune le lobe occipital et en bleu le lobe temporal.

Une premier idée de modèle pour la surface cortical peut être considérer tout le cortex, ou chaque hémisphère cérébral séparément comme une ellipsoïde. Le choix de cette forme trouve une justification dans les premières étapes du développement (les étapes de trois et cinq vésicales respectivement). Cependant, cette forme ne rend pas compte de la croissance importante du lobe temporal, qui éloigne de ellipsoïde.

En outre, la ressemblance du cortex déplié avec la forme du cortex plié, fait penser que la croissance différenciée des lobes a eu lieu dans les premières étapes du développement, qui sont suivies postérieurement d'une croissance assez homogène de toute la surface corticale.

Le modèle que l'on propose est formé par une surface générée à partir de quatre sphères, chaque sphère représentent le lobe pariétal, frontal, temporal et occipital. Ce modèle essaye de respecter la différentiation des lobes dans le développement et l'importance de chacun de ces lobes dans définition de l'allure du cortex cérébral adulte. Le diamètre de chaque sphère est déterminé en fonction de la taille de chaque lobe. Dans la figure 21 on montre la surface du modèle et les quatre sphères qui la génèrent superposée au modèle déplié.

En outre, la seule reconstruction du cortex cérébral est déjà à notre avis un intéressant outil de mesure. Des donnés importantes, comme l'aire total du cortex, la surface de chaque lobe ou l'estimation de la quantité de neurones peuvent être aisément calculés une fois que l'on a généré un modèle tridimensionnel précis. Dans notre cas, l'aire total de l'hémisphère reconstruit est obtenue par la somme des aires des triangles de la surface, et elle est d' à peu près 8.5 [dm2], avec des incertitudes dues à l'imprécision de la reconstruction.

L'étape du dépliement de la surface corticale, donne une nouvelle compréhension des donnés de IRM. Des activations qui peuvent apparaître comme voisines dans une image fonctionnelle normal, peuvent être en réalité très distantes. Avec ce type de représentation, la localisation des donnés fonctionnels, et encore plus, l'étude de ses propriétés temporelles peut acquérir une toute nouvelle clarté.

L'ensemble des données obtenues par la reconstruction et le dépliement de la surface corticale pourrait être synthétisés dans un modèle anatomo-fonctionel du type de celui que l'on propose. Les quantifications, tels que la détermination des valeurs standards des surfaces corticales; la mise en correspondance des tailles des lobes d'un cerveau plié avec un cerveau déplié et avec la taille des sphères du modèle schématique; et aussi les caractéristiques temporelles de l'organisation corticale, peuvent être ainsi comprises d'une façon unifiée. (Une idée qui semble intéressante est d'étudier la relation entre la surface cortical déplié et la forme du système ventriculaire. Etant donné que le cortex évolue à partir des parois ventriculaires, la forme de ces ventricules pourrait donner des indices sur la croissance relative des différents lobes.

d'un autre coté, l’architecture et la dynamique cortical partagent dans toute la surface corticale des lois d'une parfaite régularité. ainsi, les mécanismes sous-jacents à la compréhension du langage et à la perception visuelle seraient, au niveau cortical, essentiellement équivalentes.

l'étude qu’il est ici proposée porte sur ces aspects fondamentaux de l'organisation corticale, sur ce qui est enfin des bases biologiques de la cognition.

ce travail de recherche se veut le développement des idées esquissées dans le mémoire de dea "modèle anatomo-fonctionnel du cortex humain déplié". un modèle simple de la structure anatomo-fonctionnelle du cortex jouera le rôle d'interface entre les aspects théoriques et expérimentaux de la recherche.

à travers la modélisation mathématique comme outil de recherche théorique, nous cherchons à modéliser un système minimal d'hypothèses sur l'architecture et la dynamique de l'organisation cortical. ce modèle sera étudié et développé dans l'intention de comprendre les processus de spécialisation fonctionnel des aires corticales dans un contexte anatomique.

comme outil de recherche expérimental, on fera recours aux travaux en Imagerie par résonance magnétique (irm) qui se développent dans le laboratoire inserm-unité 483. en particulier, l'étude sur l'adaptation et plasticité des voies visuelles chez le sujet atteint de dégénérescence maculaire liée à l’âge (dmla) offre un paradigme expérimental particulièrement intéressant. la dmla se caractérise par une perte de la vision centrale par dégénérescence sénile de la macula. cette dégénérescence se traduit dans une desafférentation d'une région importante du cortex visuel. à l'aide des techniques de reconstruction et dépliement cortical à partir de données d'irm anatomique et fonctionnel, il est possible d'étudier la réorganisation d'une vaste région du cortex humain.

les données anatomiques à partir desquelles se fait la reconstruction de la surface cortical sont obtenues par irm. dans ces images il est assez simple d'obtenir une premier segmentation de la matière grise à travers la sélection de seuils appropriés. bien que cette segmentation grossière est suffissante pour les études qui cherchent la pure localisation d'une activation fonctionelle en réponse à un stimuli, elle ne permet pas l'étude physiologique du cortex comme une surface. en effet, une reconstruction tridimensionnelle de la surface corticale faite à partir d'une segmentation par seuillage peut contenir (et habituellement contient) des erreurs topologiques comme des trous ou des ponts.

la méthode de reconstruction tridimensionelle utilisée est fortement inspirée de celle proposée par jean françois mangin. la méthode peut être décomposée en 4 pas:

1. le crane est éliminé. un seuil très bas des images irm originelles permet l'obtention d'un volume tridimensionel composé du cerveau et du crane. ces deux structures sont habituellement reliées par des ponts. la contraction du volume sélectioné permet l'élimination de ces ponts. en suite, uniquement le cerveau, le plus grand volume, est conservé. le volume de départ du cerveau (reduit dans la contraction) est recupéré par une expansion conditioné à l'image irm originelle.

2. les matières grise et blanche sont marquées. le seuil qui détermine l'interface entre matière grise et matière blanche est sélectioné par inspection visuelle des images. pour chaqune de ses structures, uniquement le plus grand volume est conservé.

4. la surface du cortex est détectée. une surface est située dans l'interface gris/blanc. à travers l'expansion de cette surface s'arrive à l'obtention de la surface corticale.

si chaque pas d'expansion est conservé comme un indice associé à la surface, il est possible d'avoir une mesure de l'épaiseur de la matière grise dans chaque point de la surface corticale.

permet la sélection visuelle des seuil dans les images irm

mark

marque les voxels de l'image irm selon les seuil déterminés par setthreshold

bigconnected

pour une certaine marque, efface tous les volumes sauf le plus grand

connectaround

determine la taille du volume à partir d'un point donné

contract

un pas de contraction d'un volume

expand

un pas d'expansion d'un volume conditioné aux images irm originelles

fill

remplis les espaces vides d'un volume séleccioné. c'est à dire, tout ce qui n'appartient ni au volume ni à son plus grand complémentair

erasenot

éfface dans l'image irm tout ce qui n'est pas marqué

surface

détermination de la surface interface gris/blanc, et expansion vers la surface corticale.

le logiciel ainsi que les codes (power macintosh) peuvent être téléchargés. tout commentaire est très apprecié.

soit une matrice A qui transforme tout point p'=(h,v,w) de l'espace d'arrivée (la fenêtre) dans un point p=(x,y,z) du volume irm. la coordonnée z du point p peut être écrite comme z=(a₂₀*h + a₂₁*v + a₂₂*w). ceci permet d'écrire la transformation du volume irm vers la fenêtre de visualisation en fonction du vecteur p''=(h,v,z). le vecteur p'' contient maintenant les coordonnées de la fenêtre plus le numéro de la coupe du volume irm à visualiser. la nouvelle matrice de transformation B est cette fois:

pour la génération d'une carte qui aie les mêmes aires de la surface originale, le cortex (sphérique) est coupé le long d'un de ses méridians. chaque parallèle du cortex est aplatit et les relations angulaires de la surface corticale sont donc déformées. ce système de coordonnées coupe le voisinage de tous les points du méridian choisit pour l'applatisement.

description et figures

description et figures

description de l'algorithme d2c/dp2=0

dans des chemins alternatifs de ce projet, travaillent aussi ronald jonas, future docteur de l'école polytechnique et monsieur mpodozi de l'université du chile (auqyel je ni connais ni sais comment écrire son nom...)

en retinet, un modèle simple de la connectivité retinéene, en particulier des intéractions latérales des céllules relationnés aux trois classes chromatiques rouge, vert et bleu, réproduit plusieurs des phénomènes rélévants de la perception de la couleur. Mon travail particulier en retinet est une exploration sur le rôle de la sensibilité à la lumière et l'adaptation des intéractions latérales dans la formation de la connectivité rétinéena. Principalrment, je m' intéresse à la compréhension ecodinamique de la formation de la connectivité neuronale, c'est à dire, de sa dimension temporalle et de l'intermodification avec l'environement cognitif.